|
|
Light (Electromagnetic Radiation)
- Concept of interference, Young double slit experiment
- Review basic interference concepts here
- In order for interference to occur, the follow conditions must hold:
- the interfering light sources must be coherent. This means they must constantly maintain the same phase relationship. The light coming from the two slits in Young's double slit experiment are coherent because a single light source shines through both slits.
- the light source must be monochromatic (of single color/wavelength).
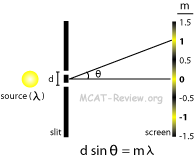
- dsinθ = mλ
- bright bands occur at m = 0, +/-1, +/-2 ...etc
- dark bands occur at m = +/-0.5, +/-1.5, +/-2.5 ...etc
- Thin films, diffraction grating, single slit diffraction
- Thin films provide a means for interference to occur.
- Light reflecting off the outer and inner boundary of a thin film interfere with each other.
- A film of oil on water has the appearance of a swirly rainbow due to this interference.
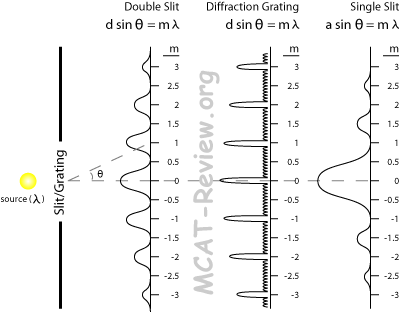
- Diffraction grating
- Diffraction = light spreads out after passing through the slit, instead of going in a straight path.
- Diffraction grating = a slab with many slits close together.
- The equation for a diffraction grating is the same as the double-slit experiment.
- dsinθ = mλ
- d is the distance between the slits, everything else is the same as the double-slit experiment.
- bright bands occur at m = 0, +/-1, +/-2 ...etc
- dark bands occur at m = +/-0.5, +/-1.5, +/-2.5 ...etc
- Single slit
- Light shining through a single slit casts a central bright band followed by a series of maximas and minimas on either side.
- The equation for a single slit diffraction is different from the equation for the double slit.
- asinθ = mλ
- a is the width of the slit.
- Maxima occurs for m = 0 (big central maxima), +/-1.5, +/-2.5 , etc.
- Minima occurs for m = +/-1, +/-2, +/-3, etc.
- Other diffraction phenomena, X-ray diffraction
- Light shining through a pin hole will not appear on the screen as a pin hole. Instead, it will be a diffraction pattern of circular bright and dark bands, with a central bright band.
- Light shining past an opaque boundary will not cast a sharp shadow of the boundary on the screen. Instead, fringes of bright and dark bands appear above the boundary.
- Light shining past a penny will not cast a completely black shadow. Instead, there will be a central bright spot, as well as patterns of bright and dark rings.
- X-ray diffraction = X-rays diffracting on a crystal. Patterns of interference that results from this is used to deduce the structure of the molecules in the crystal.
- Polarization of light
- Unpolarized light = light with electric field oscilating in many planes.
- Polarized light = light with electric field oscilating in only one plane.
- Applications of polarization:
- Selective absorption: pass light through polarizer that absorbs all but light with electric field in one plane.
- Reflection: at a certain polarizing angle, all reflected light is polarized.
- Double refraction: birefringent materials have two indices of refraction that splits the incident light into two rays polarized perpendicular to each other.
- Scattering: air molecules scatter light, which becomes polarized.
- Opticaly active molecules either rotate polarized light clockwise or counterclockwise.
- Doppler effect (moving light source or observer)
- Red shift = frequency decreases = occurs when source and observer is moving away from each other.
- Blue shift = frequency increases = occurs when source and observer is moving toward each other.
- Observed in astronomy, when stars appear redder/bluer than they really are because they are moving away/toward us.
- The equation for the doppler effect for light is the same as the doppler effect for sound, except instead of using speed of sound v, you now use the speed of light c. For red shift, use the equation for source moving away from observer. For blue shift, use the equation for source moving toward observer.
- Visual spectrum, color
- energy
- Blue = greatest energy, shortest wavelength, highest frequency.
- Red = least energy, longest wavelength, lowest frequency.
- Energy per photon = hν, where h is plank's constant and ν is frequency.
- lasers
- Laser = light amplification by stimulated emission of radiation.
- Normal light emission = spontaneous emission.
- Laser emission = stimulated emission.
- Repeated stimulated emission inside the lasing medium (by reflecting light back and forth through it) amplifies light.
Geometrical Optics
- Reflection from plane surface (angle of incidence equals angle of reflection)
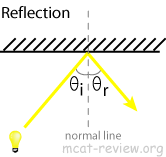
- mirrors completely reflect light.
- going from one medium to another results in partial reflection of light.
- Refraction, refractive index n, Snell's law (n1sinθ1 = n2sinθ2)
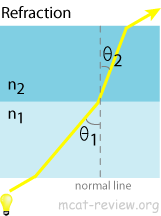
- Dispersion (change of index of refraction with wavelength)
- blue light refracts more than red light in a prism.
- white light passes through a prism and gets split into colors of the rainbow due to dispersion.
- Conditions for total internal reflection
- Going from a medium of high index of refraction to a medium of low index of refraction.
- Angle of incidence > critical angle.
- Find the critical angle by: n1sinθc = n2sin90°
- n1 > n2
- θc = critical angle
- Spherical mirrors
- Image height vs. Object distance:
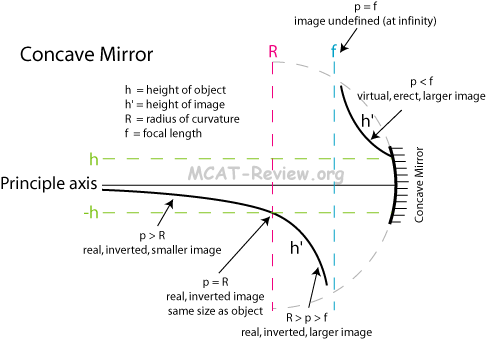
note: this curve only shows the height of the image, not the position.
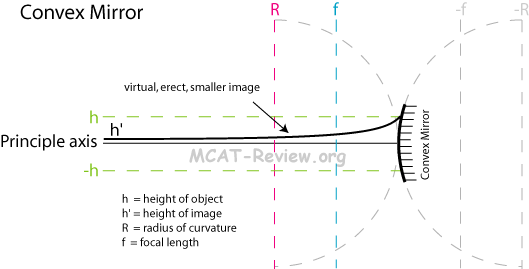
note: this curve only shows the height of the image, not the position.
- mirror curvature, radius, focal length
- mirror curvature can be concave or convex.
- concave mirrors can focus light, so it's converging.
- convex mirrors can't focus light, so it's diverging.
- The focal length is 1/2 of the radius of curvature.
- converging mirrors have positive focal length, while diverging mirrors have negative focal length.
- It's called the focal length because rays parallel to the principle axis of the mirror will converge at the focal point (for diverging mirrors, the extrapolated rays will pass through the focal point).
- use of formula (1/p) + (1/q) = 1/f with sign conventions
- For the purpose of the MCAT, p is always positive unless the MCAT explicitly tells you otherwise.
- q is positive if the image is real. For mirrors, this is when the image is in front of the mirror. For lenses, this is when the image is behind the lens.
- f is positive when the mirror/lens is converging. For mirrors, this is when the mirror is concave. For lenses, this is when the lens is convex.
- M = h'/h = -q/p, where M is magnification, h' is height of image, h is height of object.
- real and virtual images
- real images are always inverted, and can be cast on a screen.
- virtual images are always erect (noninverted), and can not be cast on a screen.
- For concave mirrors, real images (positive q) are formed in front of the mirror, where light is reflected by the mirror and can be cast on a screen. It's impossible for light to be cast behind the mirror, so anything behind the mirror is virtual (negative q).
- For convex mirrors, images are always virtual (negative q).
- Note: diverging mirrors and lenses (convex mirrors and concave lenses) can never form real images.
- Thin lenses
- You don't have to re-learn everything for lenses, because they are almost the same as mirrors:
- Convex lenses are the same as concave mirrors (both are converging) except for the following:
- Real images are on the opposite side of the lens as the object. Because light travels through the lens and can focus on a screen behind the lens.
- Virtual images are on the same side of the lens as the object. Because light can't focus in front of a lens and be cast on a screen.
- Concave lenses are the same as convex mirrors (both are diverging) except for the following:
- The virtual images formed by the lens is on the same side of the lens as the object. Because light can't focus in front of a lens and be cast on a screen.
- The image height vs. object distance curve is exactly the same as those of mirrors (convex lenses the same as concave mirrors, concave lenses the same as convex mirrors). Refer to above.
- converging and diverging lenses, focal length
- Focal length for converging lens is positive.
- Converging lens is convex.
- Focal length for diverging lens is negative.
- Diverging lens is concave.
- use of formula (1/p) + (1/q) = 1/f, with sign conventions
- same deal as with mirrors.
- p always positive.
- q positive if real, and negative if virtual.
- f positive if converging, and negative if diverging.
- real and virtual images
- Real images are inverted and can be cast on a screen.
- Virtual images are erect and can not be cast on a screen.
- For convex lenses, real images (positve q) are formed behind the lens because light passes through the lens and focuses there.
- For concave lenses, images are always virtual (negative q), and forms in front of the lens.
- lens strength, diopters
- Lens strength, or lens power is measured in diopters.
- P = 1/f
- where P is in diopters.
- lens aberration
- spherical aberrations: not all light will focus at the focal point.
- chromatic abberation: blue light gets refracted more than red light, so different colors focus differently.
- Combination of lenses
- The real image formed by a lens can be used as the object for another lens.
- Magnification by multiple lenses is the product of all the individual magnifications.
- Ray tracing
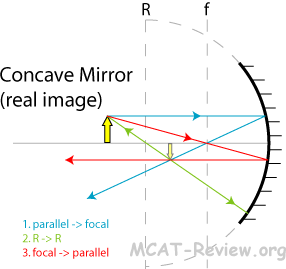
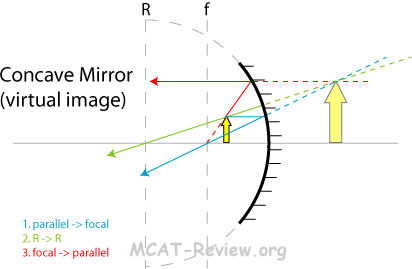
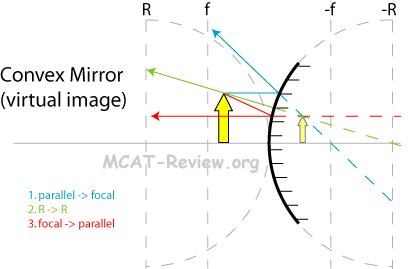
- For mirrors:
- First draw a parallel line from the object, as it bounces off the mirror, it intersects the focal point. Now, which focal point to intersect? The left or right? Use common sense: for concave mirrors, it's going to focus the ray to the left focal point. For convex mirrors, which can't focus, it's going to diverge the ray, which means you're going to have to extrapolate it to the right focal point.
- Next draw a line that intersects the R point on the principle axis. Which R? Left or right? Should I extrapolate? Again, use common sense: The ray drawn should bounce right back its original path, and not be reflected else where. By eye-balling the mirror, you should be able to figure this out.
- Now, you already have two rays drawn, and that is enough to make an intersection. Use this intersection as a guide to drawing the last ray. The last ray should first intersect the focal point, then bounce off the mirror parallel to the principle axis. Which focal point to intersect? Should I extrapolate? There's only one combination for the ray here to fit the intersection already made by the previous two rays. The trick to do this is to draw the parallel line first, and force it to intersect the intersection already made by the previous two rays.
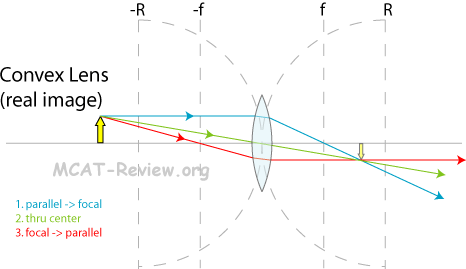
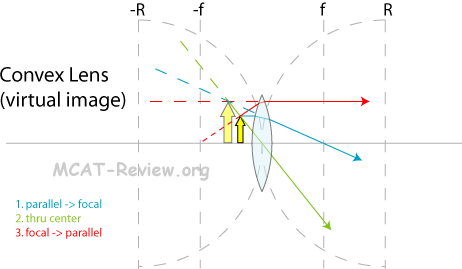
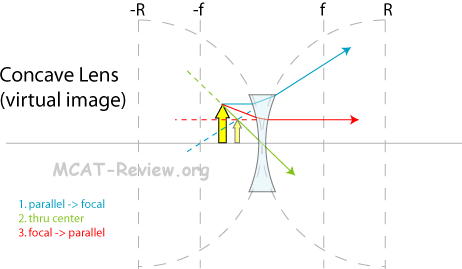
- For lenses (similar to the way you draw rays for mirrors):
- First draw the parallel → focal point ray. It should make sense which focal point the ray should hit/extrapolate given the converging/diverging nature of the lens.
- Next draw a ray intersecting the center of the lens.
- Lastly, using the intersection already made by the previous two rays as a guide, draw the focal point → parallel ray. Again, draw the parallel line first and force it to intersect the intersection already made by the previous two rays.
- Optical instruments
- Eye = lens focuses real image on retina.
- Glasses = diverging (concave) lens for near-sightedness, converging (convex) for far-sightedness.
- Magnifying glass = virtual, erect, larger image formed when p < f for a converging lens.
|
|
