Waves and Periodic Motion

Periodic motion

  • Amplitude, period, frequency
    • wave
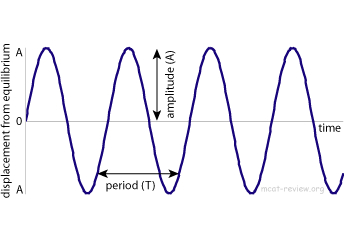
    • Amplitude (A): how high the peaks are or how low the troughs are, in meters.
      • The displacement is how far the wave vibrates / oscillates about its equilibrium (center) position.
      • The amplitude is the maximum displacement.
      • Amplitude is correlated with the total energy of the system in periodic motion. Larger amplitude = greater energy.
    • Period (T): the time it takes for one cycle, in seconds.
      • T = 1/f
    • Frequency (f): the rate, or how many cycles per second, in Hertz (cycles per second).
      • f = 1/T
      • Sometimes, frequency is in rpm (revolutions per minute). rpm = cycles per second x 60.
    • Angular frequency (w): the rate, in how many radians per second.
      • w = 2πf
      • w is also called angular velocity.
  • Phase
    • phase
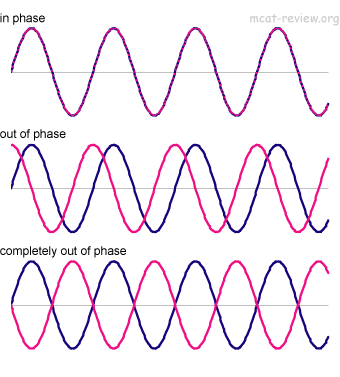
    • In phase: the waves are 0 or 2π radians (0 or 360°) apart. The resulting amplitude (sum of the waves) is twice the original.
    • Completely out of phase: the waves are π radians (180°) apart. The resulting amplitude is zero.
    • Out of phase: resulting amplitude is between 0 and twice the original.
  • Hooke's law, force F= -kx
    • F is the force that acts to restore the spring back to its equilibrium position, or restoring force.
    • k is the spring constant. Stiffer springs have a higher k value.
    • x is the displacement. The amplitude (A) is the maximum x value.
    • Potential energy = PE = ½kx2
    • Kinetic energy = KE = ½mv2
    • At the equilibrium position x = 0, PE = 0, KE = maximum.
    • At the maximum displacement (amplitude) x = A, PE = maximum, KE = 0.
    • At any point, PE + KE = maximum PE = maximum KE = constant.
    • constant = PEmax = ½kA2
    • constant = KEmax = ½mv2 at x = 0
  • Simple harmonic motion; displacement as a sinusoidal function of time
    • x = A·sin(wt)
    • x is displacement.
    • A is amplitude.
    • w is angular frequency (also called angular velocity).
    • t is time.
    • Examples of simple harmonic motion
      • Oscillating spring.
      • Pendulum.
      • Things going around a circle at constant speed (when plot the x axis position against time).
  • Motion of a spring with mass attached to its end
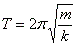
    • T=2*pi*SQRT(m/k)
    • T is period, m is the mass of the attached mass, and k is the spring constant.
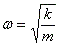
    • A simpler way to express this is: w=SQRT(k/m)
    • w is the angular frequency. The spring vibrates faster if it's stiffer and if the mass attached to it is smaller.
  • Motion of a pendulum
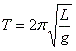
    • T=2*pi*SQRT(L/g)
    • T is period, L is the length of the string, and g is 9.8.
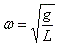
    • A simpler way to express this is: w=SQRT(g/L)
    • w is the angular frequency. The pendulum oscillates faster when gravity is large and when the string is short.
  • General periodic motion: velocity, amplitude
    • At the equilibrium position, PE = 0, KE = maximum.
    • At the maximum displacement (amplitude) x = A, PE = maximum, KE = 0.
    • At any point, PE + KE = maximum PE = maximum KE = constant.
    • constant = PEmax
      • = ½kA2 for a spring.
      • = mgA for a pendulum, where A is the maximum height that the pendulum can gain during a swing.
    • constant = KEmax = ½mv2 at the equilibrium position.
    • If you are given the velocity at the equilibrium position, then you should be able to find out the amplitude by setting maximum KE = maximum PE.
    • If you are given the amplitude, then you should be able to find out the velocity at the equilibrium position by setting maximum PE = maximum KE.

Wave Characteristics

  • Transverse and longitudinal waves
    • Transverse wave: wave displacement is perpendicular to the direction of motion.
      • Light.
      • Electromagnetic radiation.
      • A standing wave by oscillating a string side ways. The speed for such a wave = square root of (string tension / mass per unit length of the string). For the MCAT, just know that tense, light strings can produce faster transverse waves.
    • Longitudinal wave: wave displacement is parallel to the direction of motion.
      • Sound.
      • Pressure wave.
      • Earth quakes.
  • Wavelength, frequency, velocity
    • v = fλ
    • v is velocity, f is frequency, and λ is wavelength.
    • Sometimes, frequency is also written as ν.
    • Wavelength is in meters, frequency is in Hertz and velocity is in meters per second.
  • Amplitude, intensity
    • Amplitude is correlated with the energy of the wave. Greater amplitude = greater energy of the wave.
    • Intensity = energy per area per time = power per area.
    • Thus, amplitude and intensity are correlated. Greater amplitude leads to higher intensity.
    • Special note on electromagnetic waves: amplitude and intensity increases the overall energy of electromagnetic waves such as light. However, neither amplitude nor intensity changes the energy per photon. Energy per photon depends on wavelength. The shorter the wavelength (also the higher the frequency), the greater the energy.
  • Superposition of waves, interference, addition
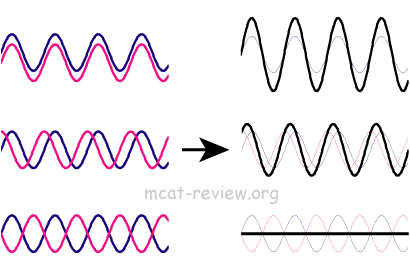
    • wave addition
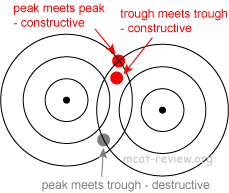
    • wave interference
    • When waves superimpose on each other, they interfere.
    • Interference results from the addition of waves.
    • When in phase waves add, the resulting wave has a greater amplitude.
    • When out of phase waves add, the resulting wave has a smaller amplitude.
    • Constructive interference: addition of waves resulting in greater amplitude.
    • Destructive interference: addition (cancellation) of waves resulting in diminished amplitude.
  • Resonance
    • Resonance is when things oscillate at its maximum amplitude.
    • Resonance occurs at resonance frequencies.
  • Resonance frequencies
    • Examples of standing waves and the resonance frequencies that produce them
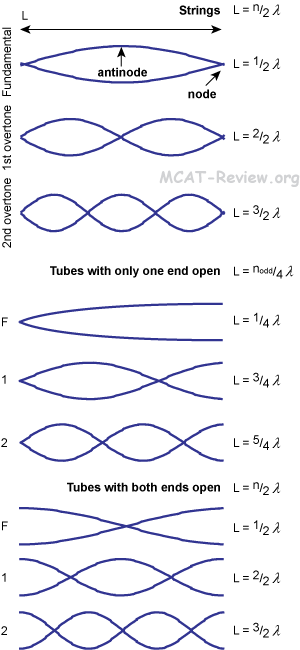
      resonance frequencies
    • Frequencies can be obtained by f = v/λ
    • Both strings and tubes open at both ends have L = n/2λ
    • Tubes with a closed end have L = n_odd/4λ
    • L is the length of the string/tube
  • Standing waves, nodes
    • Standing waves vibrate at resonance frequencies.
    • Standing waves do not propagate like other waves (that's why they're called standing waves).
    • Node: point where there's no oscillation.
    • Antinode: point where there's maximum oscillation.
  • Beat frequencies
    • Beats occur when two waves coexist at different frequencies.
    • The beat frequency is the difference between the frequencies of the two waves.
  • Refraction and diffraction
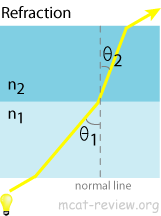
    • refraction
    • Refraction is the bending of waves when it meets a boundary between one medium to another.
      • Snell's law: n1sinθ1 = n2sinθ2 , where n is the refractive index and θ is the angle to the normal.
      • When light moves to a denser medium (higher refractive index), it bends toward the normal.
      • Dispersion, the bending of light through a prism, is a special case of refraction that separates the colors of light into a rainbow.
      • Rainbows are created by refraction by water droplets.
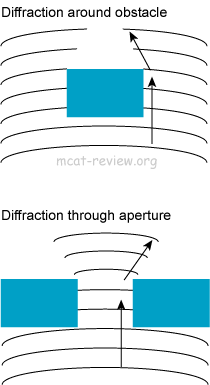
      diffraction
    • Diffraction is the spreading (diffusion) of waves around edges of apertures and obstacles.
      • You can hear sounds from the other side of a building because sound spreads.
      • Shining light through a hole will not produce a dot of light, instead, it is a diffuse circle.
      • Diffraction is the basis for the single and double slit interference experiments with light.
      • When you think of diffraction, think "diffuse".