|
|
Dimensions (length or distance, time)
- One dimension = magnitude of length or distance only.
- Two dimensions = length or distance on a 2D plane (xy coordinates).
- Three dimensions = length or distance in 3D space (xyz coordinates).
- Four dimensions = length or distance in 3D space at a given time (xyzt coordinates).
Vectors, components
- Scalar: without direction. For example, length, time, mass.
- Vector: with direction. For example, displacement, acceleration, force.
- Components: the portion of the vector in a given direction.
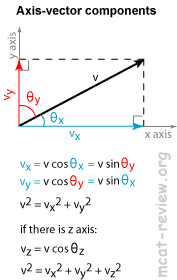
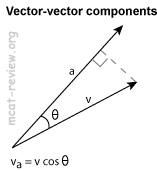
- Trigonometric rules:
- SOH CAH TOA = silly old Harry, caught a herring, trolling off Anglesea.
- SOH: sinθ = opposite / hypotenus.
- CAH: cosθ = adjacent / hypotenus.
- TOA: tanθ = opposite / adjacent.
Vector addition
- You can only directly add vectors if they are in the same direction.
- To add vectors in different directions, you must add their x, y and z components. The resulting components make up the added vector.
- The vector sum of all components of a vector equal to the vector itself.
- Operation involving a vector and a vector may or may not result in a vector (kinetic energy from the square of vector velocity results in scalar energy).
- Operation involving a vector and a scalar always results in a vector.
- Operation involving a scalar and a scalar always results in a scalar.
Speed, velocity (average and instantaneous)
- Speed: scalar, no direction, rate of change in distance.
- Velocity: vector, has direction, rate of change in displacement.
- Average speed:
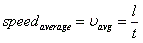
- Average velocity:
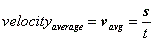
- Instantaneous speed is the speed at an instant (infinitesimal time interval).
- Instantaneous velocity is the velocity at an instant (infinitesimal time interval).
- Instantaneous speed equals instantaneous velocity in magnitude.
- Instantaneous velocity has a direction, instantaneous speed does not.
- The direction of instantaneous velocity is tangent to the path at that point.
Acceleration
- Acceleration is the rate of change in velocity
- Average acceleration:
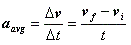
- Uniformly accelerated motion along a straight line
- If acceleration is constant and there is no change in direction, all the following applies:
- The value of speed/velocity, distance/displacement are interchangeable in this case, just keep a mental note of the direction.
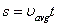
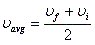
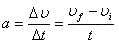
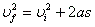
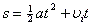
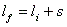
- You need to memorize those, be able to rearrange them, combine them, and how to use them.
- You need to assign one direction as + and the opposite as -, and then keep this scheme for all your calculations.
- For Cartesian coordinates, take upward and rightward motion as positive; down and left as negative.
- For free falls, take downward as positive.
- You can assign in what ever fashion you want, as long as the opposite direction is opposite in sign.
Freely falling bodies
- Free falling objects move toward the ground at constant acceleration.
- On Earth, the rate of acceleration is g, which is 9.8 m/s2.
- Whenever something is in the air, it's in a free fall, even when it is being tossed upwards, downwards or at an angle.
- For things being dropped, it's easier if you take down as positive, since that will make g positive.
- For things being tossed downwards, it's easier if you take down as positive, since that will make both initial velocity and g positive.
- For things being tossed upwards, the initial velocity will have opposite sign as g. You can take either up or down as positive depending on the question and what's convenient, but either way, initial velocity will have opposite signs as g.
- The acceleration due to gravity is constant because the force (weight) and mass of the object is constant.
- The net acceleration is a constant g if you don't take air resistance into consideration. Usually questions ignore air resistance. But if the question gives you air resistance, then the acceleration is no longer constant - it will decrease with time until it gets to zero at terminal velocity.
- When there's air resistance, the acceleration will decrease because the force (weight - resistance) is decreasing due to increasing resistance or friction at higher speeds.
- At terminal velocity, weight = friction, so the net force is 0. Thus, the acceleration is 0. So, the speed stays constant at terminal velocity.
Projectiles
- Projectiles are free falling bodies.
- The vertical component of the projectile velocity is always accelerating toward the Earth at a rate of g.
- The vertical acceleration of g toward the Earth holds true at all times, even when the projectile is traveling up (it's decelerating on its way up, which is the same thing as accelerating down).
- There is no acceleration in the horizontal component. The horizontal component of velocity is constant.
- What is the time the projectile is in the air? Ans: use the vertical component only- calculate the time it takes for the projectile to hit the ground.
- How far did the projectile travel? Ans: first get the time in the air by the vertical component. Then use the horizontal component's speed x time of flight. (Don't even think about over-analyzing and try to calculate the parabolic path).
- When you toss something straight up and it comes down to where it started, the displacement, s, for the entire trip is 0. Initial velocity and acceleration are opposite in sign.
- When you toss something straight up and it comes down to where it started, there is symmetry. Initial velocity and final velocity are equal and opposite. Time spent going up = time spent coming down.
Orbiting in space
- Satellites orbiting the Earth are in free fall.
- Their centripetal acceleration equals the acceleration from the Earth's gravity.
- Even though they are accelerating toward the Earth, they never crash into the Earth's surface because the Earth is round (the surface curves away from the satellite at the same rate as the satellite falls).
Below are old AAMC topics that has been deprecated or changed
Units and dimensions
- A unit is a label for a quantity.
- unit + unit = unit
- unit - unit = unit
- unit x unit = unit2
- unit / unit = no unit
- Dimensions are powers of units.
- unit = one dimension.
- unit2 = two dimension.
- unit3 = three dimension.
| Common SI units |
| Quantity | SI unit | Name |
| Length | m | meter |
| Area | m2 | meter squared |
| Volume | m3 | meter cubed |
| Mass | kg | kilogram |
| Density | kg/m3 | kilogram per meter cubed |
| Time | s | second |
| Speed | m/s | meter per second |
| Acceleration | m/s2 | meter per second squared |
| Force | N | Newton |
| Pressure | Pa | Pascal |
| Temperature | K | Kelvin |
| Energy | J | Joule |
| Power | W | Watt |
| Charge | C | Coulomb |
| Potential | V | Volt |
| Current | A | Ampere |
| Resistance | Ω | Ohm |
| Magnetic field | T | Tesla |
- The product of operations involving all SI units is also in SI units.
| Prefixes for units |
| Prefix | Abbreviation | Multiplier |
| exa | E | 1018 |
| peta | P | 1015 |
| tera | T | 1012 |
| giga | G | 109 |
| mega | M | 106 |
| kilo | k | 103 |
| hecto | h | 102 |
| deka | da | 101 |
| deci | d | 10-1 |
| centi | c | 10-2 |
| milli | m | 10-3 |
| micro | μ | 10-6 |
| nano | n | 10-9 |
| pico | p | 10-12 |
| femto | f | 10-15 |
| atto | a | 10-18 |
|
|
