|
|
Molecular weight
- Molecular weight is numerically equal to molecular mass (amu)
- 1 amu = 1 g/mol
- 12Carbon has 12 amu and weighs 12 g/mol
Empirical formula versus molecular formula
-
| molecular structure |
molecular formula |
empirical formula |
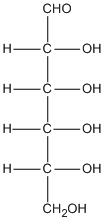 |
C6H12O6 |
CH2O |
- empirical formula is what you get after dividing everything in the molecular formula by the highest common factor.
Metric units commonly used in the context of chemistry
- Molarity = M = mol/L
- molality = m = mol/kg
- mass = kg. molar mass = g/mol.
Description of composition by % mass
- %mass = mass of species of interest / total mass * 100
Mole concept; Avogadro's number
- 1 mole = 1 mol = 1 Avogadro's number = 6.02E23 molecules
Definition of density
- density = mass / volume = kg/m3
- often in chemistry, specific gravity is used.
- specific gravity = number of times the density of water = density of substance / density of water
- density of water = 1 g/mL = 1 g/cm3
- specific gravity of water = 1 g/cm3 / 1 g/cm3 = 1
- density of lead = 11 g/cm3
- specific gravity of lead = 11 g/cm3 / 1 g/cm3 = 11
- specific gravity is unitless
Oxidation number
- common oxidizing and reducing agents
| oxidizing agents | reducing agents |
| Oxygen O2, Ozone O3, Permanganates MnO4-, Chromates CrO42-, Dichromates Cr2O72-, peroxides H2O2, lewis acids, stuff with a lot of oxygens |
Hydrogen H2, metals (such as K), Zn/HCl, Sn/HCl, LAH (Lithium Aluminium Hydride), NaBH4 (Sodium Borohydride), lewis bases, stuff with a lot of hydrogens |
- disproportionation reactions
- An element in a single oxidation state reacts to form 2 different oxidation states.
- Disproportionation can occur when a species undergo both oxidation and reduction.
- For example: 2Cu+ → Cu + Cu2+
- Here, the Cu+ acts as both oxidizing and reducing agent and simultaneously reduce and oxidize itself.
- The oxidized Cu+ becomes Cu2+
- The reduced Cu+ becomes Cu
- redox titration
- Some terms and concepts
- A = analyte = stuff with the unknown concentration that you want to find out by titration.
- Aox = analyte that is an oxidizing agent = analyte in its oxidized state.
- Ared = analyte that is a reducing agent = analyte in its reduced state.
- T = titrant = stuff that you add drip by drip to determine how much of it is needed to complete the titration.
- Tox = titrant that is an oxidizing agent = titrant in its oxidized state.
- Tred = titrant that is a reducing agent = titrant in its reduced state.
- S = standard = something with an accurately known amount or concentration. You use it in a reaction that accurately (stoichiometrically) produces a known amount or concentration of I2.
- Sox = standard that is an oxidizing agent = standard in its oxidized state.
- Sred = standard that is a reducing agent = standard in its reduced state.
- X = reactions intermediate = a species that is not present in the net equation of the overall reaction.
- Xox = intermediate that is an oxidizing agent = intermediate in its oxidized state.
- Xred = intermediate that is a reducing agent = intermediate in its reduced state.
- Iodimetric titration:
- Iodometric titration:
- 1) Aox + 2I- → Ared + I2
- 2) Tred + I2 → Tox + 2I-
- Using a standard
- Iodimetric titration with standard:
- 1) Sox + 2I- → Sred + I2
- 2) Ared + I2 → Aox + 2I-
- notes: step 1 makes sure that the I2 produced is of accurate amount/concentration by the use of the standard.
- Iodometric titration with standard:
- 1) Sox + Xred → Sred + Xox
- 2) Xox + Ared(limiting reagent) → Xred + Aox
- 3) Xox(left over) + 2I- → Xred + I2
- 4) I2 + Tred → 2I- + Tox
- notes:
- step 1 makes an intermediate of accurately known amount.
- step 2: the analyte eating up an unknown, but calculatable, amount of the intermediate.
- step 3: the remaining intermediate going on to make I2
- step 4: Here, you will find out how much T is needed to eat up all the I2 produced from step 3. From this, you'll know the amount of Xox(left over). You also can calculate the amount of Xox originally produced by the standard. Thus Xox - Xox(left over) = the amount of analyte. Important note: this is usually not a simple subtraction because you need to take stochiometric ratios into consideration.
- Iodine is used in redox titrations because in the presence of starch, I2 is dark blue while I- is colorless.
- You can only accurately titrate something going from dark to colorless ( I2 → 2I-), but not the otherway round.
- A redox titration does not necessarily need the presence of Iodine. As long as some type of color change can be seen at the equivalence point of the redox reaction, then it will work. For example:
- 5 H2O2 + 6 H+ + 2 MnO4- → 5 O2 + 2 Mn2+ + 8 H2O
- Goes from purple to colorless because of MnO4- → Mn2+ transition.
- Redox titrations are similar to acid-base titrations, except instead of measuring pH, you look for a color change.
- Practice question:
1) Sox + 5Xred → 3Sred + 3Xox
2) 3Xox + Ared(limiting reagent) → 3Xred + Aox
3) Xox(left over) + 2I- → 2Xred + I2
4) I2 + 2Tred → 2I- + Tox
after a long time doing drip by drip titration, you finally saw the dark color change to colorless. You noted down the initial and final volume reading of your pippette to be 300 mL and 200 mL, respectively. The concentration of the titrant you used was 10 M. You dissolved 1/2 mols of the standard to begin with. How much analyte was there?
- First, convert everything to mols (amount). n = MV. For the titrant (Tred) it is 10 M x (0.3 L - 0.2 L) = 1 mol
- For the standard (Sox), it is already given to you in mols. However, if it's not, you have to convert it to mols.
- We know from the notes above that Xox - Xox(left over) = the amount of analyte, after taking into account of stochiometric ratios.
- Here are the stochiometric ratios:
- From step 4
I2 : 2Tred
- From step 3
Xox(left over) : I2
- From step 2
3Xox : Ared(limiting reagent)
- From step 1
Sox : 3Xox
- Xox = 0.5 mol Sox * 3Xox / Sox = 1.5 mol Xox
- Xox(left over) = 1 mol Tred * I2 / 2Tred * Xox(left over) / I2 = 0.5 mol Xox(left over)
- For every Ared(limiting reagent), you eat up 3 Xox, thus:
Xox - 3Ared(limiting reagent) = Xox(left over)
1.5 - 3 * Ared(limiting reagent) = 0.5
Ared(limiting reagent) = 1/3 mol
- This is why you always look at the stoichiometry of the reaction in calculations. It's almost never a simple addition or subtraction.
- The reaction in the question is actually a real redox titration taken from wikipedia.
Description of reactions by chemical equations
- conventions for writing chemical equations

- Phases
- (s) = solid
- (l) = liquid
- (g) = gas
- (aq) = aqueous (dissolved in water)
- Coefficient
- an equation with coefficients is a balanced equation.
- Direction
- A single head arrow denotes the reaction goes to completion in the direction of the arrow.
- A double-sided arrow denotes a reaction in equilibrium.
- A double-sided arrow with one side larger than the other denotes an equilibrium in favor of the side of the larger arrow.
- Charge
- Denotes charge and magnitude, for example +, -, 2+, 5- ...etc.
- Neutral charges are not denoted.
- balancing equations, including oxidation-reduction equations
- balance the combustion of propanol: C3H8O + O2 → CO2 + H2O
- pick out the atom (or group) that is the easiest to balance (usually represented in only 1 term on both side of the equation. In this case it is carbon.
C3H8O + O2 → 3CO2 + H2O
- The next easiest to balance is hydrogen
C3H8O + O2 → 3CO2 + 4H2O
- Leave the hardest to last, oxygen. O is present in every term of the equation, so if we tried to balance O first, we'd be having a hard time. However, now that we balanced every other term, this leaves only one term left that contains O and that we haven't balanced yet. Do a quick count of oxygen atoms: there's 1 from C3H8O, 3x2 from 3CO2, and 4x1 from 4H2O. Set up this equation: 1 + 2x = 3x2 + 4x1, where x would be the coefficient of our last term, O2. Solve for x
C3H8O + 9/2O2 → 3CO2 + 4H2O
- Even though we balanced out every term, we're not done yet. We need to get rid of any fractions, so multiply every term by 2.
2C3H8O + 9O2 → 6CO2 + 8H2O
- Balancing oxidation-reduction (redox) equations
- Separate into half reactions.
- There will be 2 half equations: one will be oxidation, the other reduction.
- Half equations contain only species of interest - those containing the atom that undergoes a change in oxidation state.
- Anything that is not covalently attached to the atom is not part of the species of interest.
- Anything that does not undergo a change in oxidation state is a spectator ion/species.
- Balance each of the half reactions.
- Balance both charge and atoms.
- To balance one oxygen atom:
- Under acidic conditions: add H2O to the side that needs the oxygen atom, then add H+ to the other side.
- Under basic conditions: add 2OH- to the side that needs the oxygen atom, then add H2O to the other side.
- The Ion-Electron Method: you balance out the atoms first, then charge.
- The Oxidation-State Method: treat the species of interest as a single atom (those that undergo a change in oxidation number) and then balance it.
- Recombine the half reactions.
- Multiply each half reaction by a factor, such that when you add them together, the electrons cancel out.
- It's like you're trying to solve a simultaneous equation and you want to eliminate the electron term.
- Finishing touches
- Combine any idendical species on the same side of the equation.
- Cancel out any identical species on opposite sides of the equation.
- Add back in the spectator ions.
- For the oxidation-state method, now is also the time to balance out the oxygens and hydrogens.
- Check to make sure that both sides of the equation have equal number of atoms and neutral net charge.
- Example using ion-electron method: K2Cr2O7 (aq) + HCl (aq) → KCl (aq) + CrCl3 (aq) + H2O (l) + Cl2 (g)
- Separate into half reactions.
- Reduction: Cr2O72- → Cr3+
- Oxidation: Cl- → Cl2
- Species of interest for the oxidation reaction is Cl-, not HCl, because the H+ is not covalently attached to our atom of interest, and the hydrogen proton breaks off in aqueous solution.
- Similarly, we use Cr2O72- and not K2Cr2O7
- K+ is the spectator ion.
- Balance each of the half reactions.
- The Ion-Electron Method: you balance out the atoms first, then charge.
- Balancing atoms for the reduction half reaction (Ion-electron method):
- Cr2O72- → Cr3+
- Cr2O72- → 2Cr3+
- Cr2O72- + 14 H+ → 2Cr3+ + 7H2O
- Balancing charge for the reduction half reaction (Ion-electron method):
- Cr2O72- + 14 H+ + 6e- → 2Cr3+ + 7H2O
- Do the same thing for the oxidation half reaction (Ion-electron method):
- Cl- → Cl2
- 2Cl- → Cl2
- 2Cl- → Cl2 + 2e-
- Recombine the half reactions.
- Cr2O72- + 14 H+ + 6e- → 2Cr3+ + 7H2O
- 2Cl- → Cl2 + 2e-
- Multiply everything in the second equation by 3
- 6Cl- → 3Cl2 + 6e-
- Add the two equations together
- Cr2O72- + 14 H+ + 6e- + 6Cl- → 2Cr3+ + 7H2O + 3Cl2 + 6e-
- Finishing touches
- Except for the electrons, there are no like terms to combine or cancel at this time...
- Cr2O72- + 14 H+ + 6Cl- → 2Cr3+ + 7H2O + 3Cl2
- For the ion-electron method, the equation is already balanced at this stage of the game. However, you need to add back in the spectator ions. When adding back the spectator ions, what ever you do to the left side, you do to the right.
- To the left side: The dichromate came in counter-ioned with K+, so add 2 K+.
- To the right side: What ever you do to the left side, you do the same to the right side.
- K2Cr2O7 + 14 H+ + 6Cl- → 2Cr3+ + 7H2O + 3Cl2 + 2K+
- Referring back to the original equation, the Hs and Cls on the left came in as HCl, so in order to balance the extra 14 - 6 = 8 Hs, you add 8 Cls. As always, if you add 8 Cls to the left, go ahead and add the same to the right.
- K2Cr2O7 + 14 HCl → 2Cr3+ + 7H2O + 3Cl2 + 2K+ + 8Cl-
- We're done focusing on the left side. A quick look at the right side shows that we need to combine 2 of the Cl- with the 2 K+, and the remaining 6 Cl- goes with the Cr. Thus the final balanced redox equation is:
- K2Cr2O7 (aq) + 14 HCl (aq) → 2CrCl3 (aq)+ 7H2O (l) + 3Cl2 (g) + 2KCl (aq)
- Example using oxidation-state method: K2Cr2O7 (aq) + HCl (aq) → KCl (aq) + CrCl3 (aq) + H2O (l) + Cl2 (g)
- Separate into half reactions (same as the ion-electron method).
- Reduction: Cr2O72- → Cr3+
- Oxidation: Cl- → Cl2
- Balance each of the half reactions.
- The Oxidation-State Method: you focus on the atom of interest.
- Balancing the atom of interest for the reduction half reaction (Oxidation-state method):
- Cr2O72- → Cr3+
- Cr2O72- → 2Cr3+
- Each oxygen is 2- so the 2 Cr on the left must be 6+
- 2Cr6+ → 2Cr3+
- Balancing charge for the atom of interest in the reduction half reaction (Oxidation-state method):
- 2Cr6+ + 6e- → 2Cr3+
- Do the same thing for the oxidation half reaction (Oxidation-state method):
- Cl- → Cl2
- 2Cl- → Cl2
- 2Cl- → 2Cl0
- 2Cl- → 2Cl0 + 2e-
- Recombine the half reactions.
- 2Cr6+ + 6e- → 2Cr3+
- 2Cl- → 2Cl0 + 2e-
- Multiply everything in the second equation by 3:
- 2Cr6+ + 6e- → 2Cr3+
- 6Cl- → 6Cl0 + 6e-
- add the two equations together
- 2Cr6+ + 6e- + 6Cl- → 2Cr3+ + 6Cl0 + 6e-
- Finishing touches
- Except for the electrons, there are no like terms to combine or cancel at this time...
- 2Cr6+ + 6Cl- → 2Cr3+ + 6Cl0
- Convert the atoms of interest into species of interest by referring back to the original equation.
- K2Cr2O7 + 6HCl → 2CrCl3 + 3Cl2
- Now unlike the ion-electron method, where the equation is balanced and you only add back spectator ions at this stage of the game, the oxidation-state method requires you to balance the equation again. This is because after you convert the atoms of interest back to their species of interest, the equation is no longer balanced.
- Start with the oxygens. On the left you have 7 O, so add 7 H2O to the right.
- K2Cr2O7 + 6HCl → 2CrCl3 + 3Cl2 + 7H2O
- Now take care of the hydrogens. You have 6H on the left, but 14H on the right. That means you should add 8 more Hs to the left to make a total of 14. All 14 Hs on the left should be in the form of HCl (refer back to the original equation. Note, HCl here is both the species of interest and also the spectator species. Some of the HCl contributes to the Cl- → Cl2 oxidation, but the other portion of the HCl doesn't undergo redox. It merely provides the H+ for the water and the Cl- for the KCl and CrCl3).
- K2Cr2O7 + 14HCl → 2CrCl3 + 3Cl2 + 7H2O
- Now you see there's 14 Cl to the left, and 12 Cl to the right. You need 2 more Cls on the right. Referring back to the original equation, all the right-sided Cls come in the form of KCl (don't modify the Cl2 since you've already correctly balanced it by the oxidation state method. When balancing equations at this stage, only play around with water and the spectator species).
- K2Cr2O7 + 14HCl → 2CrCl3 + 3Cl2 + 7H2O + 2KCl
- Upon examination of the equation, every atom is balanced. So the final balanced redox equation is:
- K2Cr2O7 (aq) + 14HCl (aq) → 2CrCl3 (aq) + 3Cl2 (g) + 7H2O (l) + 2KCl (aq)
- limiting reactants
- Limiting reactant is the reactant that will get all used up first.
- What is the limiting reactant for the following reaction?
- 3Xox + Ared → 3Xred + Aox
- Given: You use 60 grams of Xox and 63 grams of Ared
- Given: the molecular weight of Xox is 2 amu, and Ared is 7 amu.
- The first thing you do is convert everything in moles. 1 amu = 1 g/mol.
- Xox: 60 g / 2 amu = 30 mols.
- Ared: 63 g / 7 amu = 9 mols.
- Now here's where stoichiometry comes in: divide the mols by the stoichiometric coefficient of the species:
- 30 mols / 3 = 10 for Xox
- 9 mols / 1 = 9 for Ared
- Now compare the values. 9 is the smallest, so Ared is the limiting reactant.
- Limiting reactant can also be called the limiting reagent, limiting species, limiting [whatever].
- theoretical yields
- The theoretical yield is how much of the product will be made based on stoichiometry.
- In calculating the theoretical yield, first find out what your limiting reactant is. Then, use your limiting reactant as the stoichiometric basis to calculate how much product you will get.
- In real life, the experimental yield is always less than the theoretical yield because of loss during steps of the reaction (now you can have a higher experimental yield if you're in a chem lab and you accidentally dumped in more reactants than you realized).
- What is the theoretical yield for 3Xred
3Xox + Ared → 3Xred + Aox
if you react 60 grams of Xox with 63 grams of Ared given that the molecular weight of Xox is 2 amu, Ared is 7 amu, and Xred is 10 amu?
- First, find who's the limiting reagent.
- Using the method described above in the limiting reactant section, we find out that Ared is the limiting reactant.
- Next, take the amount in mols of the limiting reactant (9 mols according the the above calculation) and do the stoichiometry to get to how many mols of 3Xred this will yield.
- 9 mols of Ared * 3 mols of Xred per 1 mol of Ared = 27 mols.
- Lastly, convert mols to grams: 27 mols * 10 g/mol = 270 g
- The theoretical yield for the above reaction is 270 g of Xred
- Say you did an actual experiment of the above reaction and you managed to obtain 243 g Xred, then the experimental yield is 243 g.
- Percent yield = experimental yield / theoretical yield x 100
- For the above experiment, the percent yield would be 243 / 270 x 100 = 90 %
|
|


