Phases and Phase Equilibria

Gas phase

Absolute temperature, K scale

	K	°C	°F
Absolute zero	0	-273	-460
Freezing point of water / melting point of ice	273	0	32
Room temperature	298	25	77
Body temperature	310	37	99
Boiling point of water / condensation of steam	373	100	212

K = °C + 273
F = °C x 1.8 + 32

Pressure, simple mercury barometer

Pressure is the force exerted over an area: P = F/A
Due to gravity, the atmosphere exerts a pressure of 101 kPa at sea level. For convenience, 101 kPa = 1 atm.
Pressure decreases at higher elevations.
The mercury barometer measures atmospheric pressure by allowing the atmospheric pressure to "push" on a column of mercury.
The barometer is open at one end and closed off (vacuum) at the other.
The atmosphere "pushes" at the open end, which results in the mercury rising up in the closed end.
The measured atmospheric pressure P = F/A. F is the weight of the mercury that got pushed up and A is the cross-section area of the column that the mercury got pushed through.
Standard mercury barometers are calibrated such that 1 atm of pressure will push the mercury up by 760 mm. For convenience, mm Hg is also called the Torr. So, you don't have to do the P=F/A calculation to find out the pressure reading from a barometer. Just know that 1 atm = 760 mm Hg = 760 torr.
1 atm = 101 kPa = 101,000 Pa = 760 mm Hg = 760 Torr.
When performing P = F/A calculations, make sure that F is in Newtons, A is in meter squared and the resulting P will be in Pascals. You can then convert the Pascals to whatever units the answer choices are in.

Molar volume at 0 degrees Celsius and 1 atm = 22.4 L/mol

You must memorize this: ideal gases occupy 22.4 L per mol of molecules.
Do not get this mixed up - it is 22.4 liters per mole, not the other way around.
The way to remember this is that the mol is a huge number - 6.02E23 molecules. These gazillions of molecules occupy a lot of space - 22.4 L to be exact.
Another way you can remember this is to look at the periodic table: Air is made up mostly of nitrogen, which has an atomic mass of 14. In the diatomic form, N₂ weighs 14x2 = 28 grams per mol. Now, air is really light. In order for you to grab 28 grams of air, you need more than just a bottle of air, you need a huge tank totaling 22.4 L.

Ideal gas

definition
- An ideal gas consists of pointy dots moving about randomly and colliding with one another and with the container wall. The ideal gas obeys the kinetic molecular theory of gases and has the following properties.
  - Random molecular motion.
  - No intermolecular forces.
  - No (negligible) molecular volume.
  - Perfectly elastic collisions (conservation of total kinetic energy).
- You can treat gases as ideal gases at:
  - Low pressures
  - High temperatures
- Deviation from the ideal occurs at high pressure and low temperature. At these conditions, the gas molecules are "squished" together. When the gas molecules are so close together, they experience intermolecular interactions. Also, the molecular volume becomes significant when the total volume is squished down so much. The intermolecular attractions will cause collisions to be sticky and inelastic. At the extremely high pressures and low temperatures, gases cease to be gases at all - they condense into liquids.
- Ideal gases behave according to the ideal gas law.
ideal gas law PV=nRT, where P is pressure, V is volume, n is # mols of gas, R is the gas constant, and T is temperature.
- Combined gas law:
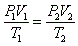
  - Because nR is constant (n is the # mols and R is the gas constant), PV/T must also be constant.
  - Boyle's law and Charles' law can all be derived from the combined gas law.
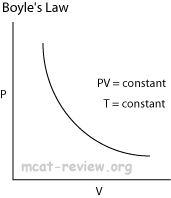
- Boyle's law: at constant temperature, P₁V₁ = P₂V₂
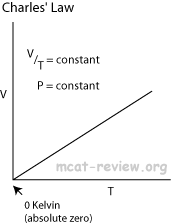
- Charles' law: at constant pressure,
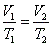
- Charle's law extrapolates to absolute zero, where volume also goes to zero (this is only an extrapolation).
- Avogadro's law: Equal volumes of two gases will also contain equal number of mols of each gas (given ideal conditions: ideal gas at STP).
  - PV = nRT
  - R is constant, and at STP, pressure and temperature is also constant.
  - V/n = RT/P
  - If you plug in STP values, you'll end up with V/n = 22.4 L/mol.
  - All ideal gases at STP will occupy 22.4 L per mol of gas molecules.

Kinetic molecular theory of gases

The ideal gas laws can be derived from the kinetic theory of gases.
The kinetic theory holds the following assumptions
- Random molecular motion.
- No intermolecular forces.
- No (negligible) molecular volume.
- Perfectly elastic collisions (conservation of total kinetic energy).
The kinetic theory holds the following concepts:
- Pressure of a gas is due to its molecules constantly colliding with the walls of its container.
- Pressure is equally distributed over the walls of the container because molecular motion is random.
- Temperature is a measure of the average kinetic energy of the gas molecules.
- Higher temperature means the molecules are traveling faster, lower temperatures means slower molecules.
Diffusion and Effusion
- Diffusion: random molecular motion, causing a substance to move from an area of higher concentration to an area of lower concentration (diffusion down its concentration gradient).
- Effusion: random molecular motion, causing a substance to escape a container through a very small openning.
- Graham's Law (applies both to diffusion and effusion for the purposes of the MCAT).
  - ^Rate₁/_Rate₂ = √^M₂/_M₁
  - Rate = rate of diffusion or effusion. M = molecular weight of gas molecule.
  - A possible question on the MCAT is two gasses diffuse down a tube from opposite ends. Where will the gases meet? The gist of this is that the lighter gas will travel faster, and the gases will meet at a point that is farther from the end of the lighter gas.
- Graham's Law is derived from the Kinetic theory
  - Temperature = average kinetic energy
  - At a given temperature all gases have the same kinetic energy.
  - ½m₁v₁² = ½m₂v₂²
  - m₁v₁² = m₂v₂²
  - ^v₁²/_v₂² = ^m₂/_m₁
  - ^v₁/_v₂ = √^m₂/_m₁

Deviation of real-gas behavior from ideal gas law

qualitative
- When molecules are far apart (under conditions of low P, high T), they are ideal.
- When molecules are brought close together (higher P, lower T), they experience intermolecular attraction.
- When molecules are brought so close together that they clash into one another, they experience steric repulsion.
quantitative (Van der Waals' equation)
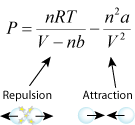
- b for bounce. The term with the constant b is the repulsion term. The greater b is, the more repulsion, which leads to greater pressure.
- a for attraction. The term with the constant a is the attraction term. The greater a is, the more attraction, which leads to less pressure.

Partial pressure, mole fraction

Partial pressure = a component of the total pressure exerted by a species in a gas mixture.
The total pressure of a mixture of gas = The sum of all the partial pressures.
Mole fraction = a component (fraction) of the total # mols that belongs to a species in a gas mixture.
Mole fraction for species A = # mols of A / # mols of the entire gas mixture. = # mols of A / Σ # mols of A, B, C ...
Dalton's law relates partial pressure to mole fraction.

Dalton's law relating partial pressure to composition

P_i = χ_i·P_total
P_total = ΣP_i = Σχ_i·P_total
P_total is total pressure.
P_i is partial pressure of species i.
χ_i is the mole fraction of species i.

Liquid phase: intermolecular forces

Hydrogen bonding

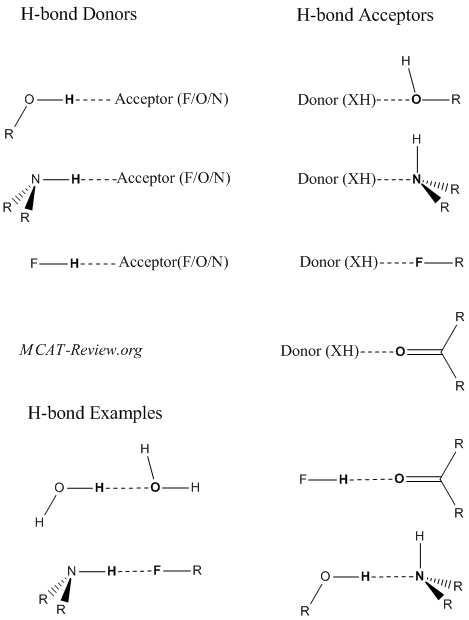
Hydrogen bonding is a weak interaction between a partially positive H and a partially negative atom.
Technically, hydrogen bonds are a special type of dipole-dipole interaction.
Hydrogen bonding increases the boiling point.
Partially positive H are also called hydrogen bond donors. They are hydrogens that are bonded to either F, O, or N.
Partially negative atoms are also called hydrogen bond acceptors. They are most commonly F, O, or N.
Do ethers form hydrogen bonds with other ethers? Ans: no, because ethers do not have a partially positive H (donor).
The more polar a bond is, the stronger the hydrogen bond. The H-F bond is the most polar, followed by the H-O bond, and lastly the H-N bond.

Dipole interactions

All polar molecules exhibit dipole-dipole interactions. This is where the polar molecules align such that opposites attract.
Dipole-dipole interactions increase the boiling point, though not as significantly as hydrogen bonding.
Dipole interactions are stronger the more polar the molecule is.
Ion-dipole interactions are similar to dipole-dipole interactions, but it's stronger because it is no longer an interaction involving just partial charges. Instead, it is an interaction between a full charge (ion) and a partial charge (dipole).
Ion-dipole interactions get stronger when you have larger charge magnitude of the ion, and large polarity of the dipole molecule.

Van der Waals' forces (London dispersion forces)

Also called dispersion forces.
Dispersion forces exists for all molecules, but are only significant for non-polar molecules. For polar molecules, dipole forces are predominant.
Dispersion forces result from induced and instantaneous dipoles.
Induced dipoles: when a polar molecule interacts with a non-polar molecule, then polar molecule induces a dipole in the non-polar molecule.
Instantaneous dipoles: Non-polar molecules have randomly fluctuating dipoles that tend to align with one another from one instant to the next.
Dispersion forces get stronger for larger molecules. For example, decane (C₁₀H₂₂)has a stronger dispersion force than ethane (C₂H₆).

Phase equilibria

Phase changes and phase diagrams

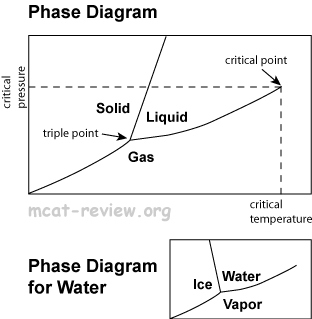
Solid: atoms/molecules vibrate about a fixed position. Hard to compress. Does not flow to fill a container.
Liquid: atoms/molecules move about, but are close together and bound by intermolecular forces. Hard to compress. Flows to fill a container.
Gas: atoms/molecules fly about far apart from one another and do not experience intermolecular forces. Easy to compress. Flows to fill a container.
Solid-liquid boundary: solid and liquid exist in equilibrium.
Solid-gas boundary: solid and gas exist in equilibrium.
Liquid-gas boundary: liquid and gas exist in equilibrium.
Triple point: the temperature and pressure at which all three phases of matter coexist in an equilibrium.
Critical point: the temperature and pressure at which liquids and gases become indistinguishable.
Critical temperature: the temperature above which you can no longer get a liquid no matter how much pressure you press on it.
Water phase diagram is different from others because the solid-liquid boundary is slanted to the left. This is because water (liquid) is more dense than ice (solid), and if you increase the pressure at a given temperature, then you turn ice into water.
Mnemonic for remembering which section of the phase diagram is for gases: "gas comes out this way."

Freezing point, melting point, boiling point, condensation point

Freezing point: temperature (at a given pressure) that liquids begins to freeze into a solid.
Melting point: temperature (at a given pressure) that a solid begins to melt into a liquid.
Boiling point: temperature (at a given pressure) that a liquid begins to turn into a gas.
Condensation point: temperature (at a given pressure) that a gas begins to condense into a liquid.
Freezing point and melting point are the same, they can both be found along the solid-liquid phase boundary.
Boiling point and condensation point are the same, they can be found along the liquid-gas boundary.
Sublimation: conversion of a solid directly into a gas. Conditions for sublimation can be found along the solid-gas boundary.

Molality

Molality is a measure of the concentration of solutes in a solvent.
Molality is given the symbol m (don't confuse the small case m with the large case M that is molarity)
Molality = mols of solute / mass (in kg) of solvent.
Compare molality (mol solute/kg solvent) to molarity (mol solute/L solution).

Colligative properties

Colligative properties = properties that depend on the # of solute particles, but not on the type.
Solute particles in solution like to keep the solution in liquid phase. This is why it makes it harder to boil (raises its boiling point) and also makes it harder to freeze (lowers the freezing point). Lowering the vapor pressure is just another fancy name for raising the boiling point.
Van't Hoff Factor (i): all colligative properties take into consideration of the Van't Hoff factor. Basically, it means convert concentration to reflect the total number of particles in solution. For example, glucose has i of 1 because it doesn't break up in solution. NaCl has i of 2, because in solution, it breaks up into 2 particles Na⁺ and Cl^-.
- vapor pressure lowering (Raoult's law)
  - P = χ_solvent·P°_solvent
  - ΔP = χ_solute·P°_solvent
  - P is the vapor pressure.
  - ΔP is the decrease in vapor pressure.
  - χ_solute = mol fraction of the solute = # mols of solute / # total mols of both solute and solvent
  - χ_solvent = mol fraction of the solvent = # mols of solvent / # total mols of both solute and solvent
  - P°_solvent is the vapor pressure of the pure solvent alone.
  - When you are calculating χ_solute, make sure you take into account of van't Hoff. ie. 1 mols of NaCl in solution is actually 2 mols of particles.
- boiling point elevation (deltaTb = kb*m *i)
  - ΔT_b = k_b·m·i
  - ΔT_b is the increase in boiling point.
  - k_b is the molal boiling point constant (like almost every other constants, the MCAT will give it to you).
  - m is the molality (mol solute/kg solvent).
  - i is van't Hoff factor.
- freezing point depression (deltaTf = -kf*m *i)
  - ΔT_f = -k_f·m·i
  - ΔT_f is the decrease in freezing point (the negative sign shows that the change is a decrease).
  - k_f is the molal freezing point constant.
  - m is the molality (mol solute/kg solvent).
  - i is van't Hoff factor.
- osmotic pressure
  - π = MRT *i
  - π is the osmotic pressure.
  - M is the molarity in mol/L.
  - R is ideal gas constant.
  - T is the temperature in K.
  - Osmotic pressure determines whether and in what direction osmosis will occur.
  - Osmosis is the movement of solvent across a semi-permeable membrane from an area of low solute concentration (high solvent concentration) to an area of high solute concentration (low solvent concentration).
  - Solvent will move from an area with low π value to an area with high π value.

Colloids

Solution: things are mixed at the molecular level and will always stay mixed. When you use the term dissolve, you are making a solution.
Colloids: things are mixed at a "semi-molecular level" with solute aggregates that are really really tiny. Colloids will stay mixed until you centrifuge it.
Suspension: things are mixed at a particle level and will NOT stay mixed.
The famous colloid example is milk. Also, when you shake water and oil vigorously, you can get an emulsion, which is a colloid.

Henry's Law

P_solute = k [solute]
P_solute is the partial pressure of the solute at the solution's surface.
k is a constant.
[solute] is the solute concentration in solution.
The partial pressure of a solute just above the solution's surface is directly proportional to its concentration.