Fluids and Solids

Fluids

• Liquids and gases are fluids.
• Density, specific gravity
  • Density: ρ=m/V, where ρ is density, m is mass, and V is volume.
  • The density of water is ρ_water = 1 g/mL = 1 g/cm³ = 1 kg/L.
  • Specific gravity is the density of something compared to water.
  • Specific gravity = ρ/ρ_water.
  • The specific gravity of water is 1.
• Buoyancy, Archimedes' principle
  • 
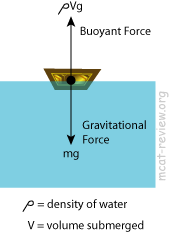
  • Archimedes' principle: buoyant force on an object = weight of the fluid displaced by the object.
  • F_B = weight_displaced = m_displacedg =ρ_fluidV_submergedg
  • The volume of an object that is submerged = the volume of fluid displaced by the object.
  • Things float when F_B = Weight.
  • Things will rise upward when F_B > Weight.
  • Things will sink when F_B < Weight.
• Hydrostatic pressure
  • Pascal's law: if you apply pressure on a liquid, the pressure is transmitted equally to all parts of the liquid.
    • 
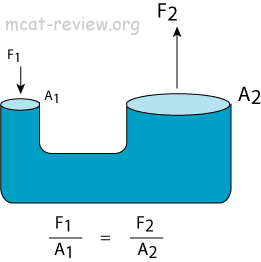
    • F₁/A₁ =F₂/A₂
    • The pressure input at one end is the same as the pressure output at the other.
    • You apply a small force over a small area, and the output force at the end with the larger area will be greater.
    • A₁d₁=A₂d₂, where d is the distance that the end moves.
    • The work done on one end is the same as the work output at the other.
  • P = pgh (pressure vs. depth)
    • P=ρgh
    • P is pressure, ρ is the density of the fluid; g is the gravitational constant, h is the height from the surface, or depth that the object is submerged.
    • Pressure at the surface is 0 because h = 0.
    • Pressure at a depth of h is ρgh.
    • ρgh is the gauge pressure because it ignores the atmospheric pressure above the fluid.
    • Absolute pressure of something submerged in the ocean = ρgh + atmospheric pressure.
• Viscosity: Poiseuille flow
  • When a viscous fluid flows through a pipe, the flow has a front that is shaped like a parabola bulging outward.
• Continuity equation (A·v = constant)
  • The volume flow rate of a fluid is constant.
  • dV/dt = constant, where dV/dt is volume flow rate.
  • dV = A·dL
  • A·dL/dt = A·v = constant, where v is linear flow rate (velocity).
• Concept of turbulence at high velocities
  • Low velocity -> laminar flow.
  • High velocity -> turbulent flow, forms eddies.
• Surface tension
  • Surface tension gives the surface of a liquid the ability to support things that are very light.
  • For example, insects can walk on water due to surface tension.
  • Surface tension is due to the attraction between the molecules of the solvent.
• Bernoulli's equation
  • P + ½ρv² + ρgh = constant

Solids

• Density: ρ=m/V, where m is mass and V is volume.
• Elastic properties (elementary properties)
  • 
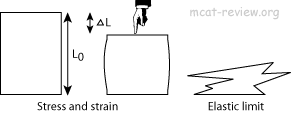
  • Stress: the pressure exerted on an object. σ = stress = F/A.
  • Strain: the deformation of the object in the direction of the applied force divided by the original length. ε = strain = ΔL/L₀.
  • Young's modulus = stress / strain.
  • Young's modulus, the ratio between stress and strain, is constant until you reach the elastic limit, where things get permanently deformed.
• Elastic limit: The maximum stress something can handle before it breaks or become permanently deformed.
• Thermal expansion coefficient
  • Things expand when temperature rises, and contract when temperature falls.
  • ΔL = αL₀ΔT
  • ΔL is the change in length, L₀ is the initial length, ΔT is the change in temperature, and α is the coefficient of linear expansion.
  • In the same fashion as linear expansion, the equations for volume and area expansions are below.
  • ΔV = βV₀ΔT
  • ΔA = γA₀ΔT
• Shear
  • 
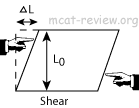
  • Shear = stress / shear ratio.
  • Shear ratio = ΔL/L₀.
  • When ΔL is very small compared to L₀, Shear ratio is approximately the same as the shear angle.
  • Shear angle = tan^-1ΔL/L.
  • Note: ΔL and L are perpendicular to each other.
• Compression: solids and liquids are generally not compressible. Gasses are compressible.