Electronic Circuit Elements

Circuit elements

• Current (I = ΔQ/Δt, sign conventions, units)
  • 
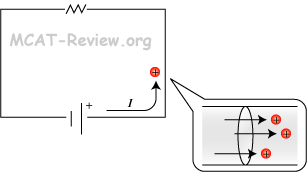
  • Current is the rate of charge flow through the cross-section of a conductor (wire).
  • Traditionally, the direction of current is taken as the flow of positive charges.
  • The unit for current is Coulombs per second, C/s.
• Battery, electromotive force, voltage
  • Electromotive force (emf) is really not a force, but a potential difference, with the unit voltage.
  • A battery is a source of emf.
  • If the battery has no internal resistance, then potential difference across the battery = EMF.
  • If the battery has internal resistance, then potential difference across battery = EMF - voltage drop due to internal resistance.
• Terminal potential, internal resistance of battery
  • 
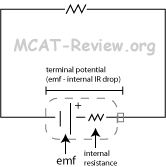
  • Terminal potential is the voltage across the terminals of a battery.
  • Internal resistance of a battery is like a resistor right next to the battery connected in series.
  • Terminal potential = EMF - IR_internal
• Resistance
  • Ohm's law (I = V/R)
  • resistors in series
    • 
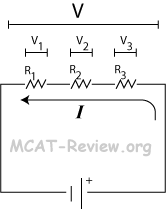
    • I_series = I₁ = I₂ = I₃
    • All resistors in series share the same current.
    • V_series = V₁ + V₂ + V₃
    • Voltage drop among resistors in series is split according to the resistance - greater resistance, greater voltage drop (V = IR).
  • resistors in parallel
    • 
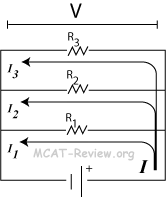
    • V_parallel = V₁ = V₂ = V₃
    • All resistors in parallel share the same voltage.
    • I_parallel = I₁ + I₂ + I₃
    • Current among resistors in parallel is split according to the resistance - greater resistance, less current (I = V/R).
  • resistivity (ρ = RA/L)
    • Resistivity is the inverse of conductivity.
    • Greater resistivity, greater resistance of the material.
    • Rearranging the above equation to get R = ρL/A. To make a wire of low resistance, select a material that has low resistivity, keep the wire short, and keep the diameter of the wire large.
    • Extension cords are made really thick to keep the resistance down, so it doesn't heat up and cause a fire.
• Capacitance
  • concept of parallel-plate capacitor
    • 
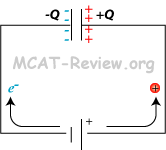
    • C = Q/V = εA/d
    • Greater capacitance is created by a greater charge on plates (Q) for a given voltage (V), greater plate area (A), or smaller distance between plates (d).
    • V = Ed, where V is voltage across capacitor, E is electric field between capacitor, and d is the distance between capacitor plates.
  • energy of charged capacitor
    • U = ^Q2/_2C = ½QΔV = ½C(ΔV)²
    • U is the potential energy of the charged capacitor, Q is charge stored (magnitude of either +Q or -Q on one of the plates), C is capacitance.
  • capacitors in series
    • 
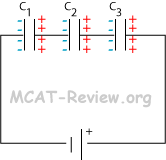
    • ¹/_Ceq = ¹/_C1 + ¹/_C2 + ¹/_C3
  • capacitors in parallel
    • 
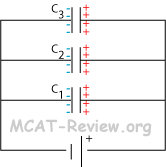
    • C_eq = C₁ + C₂ + C₃
  • dielectric
    • Dielectric = nonconducting material.
    • Inserting a dielectric between the plates of a capacitor increases the capacitance by either increasing Q (if V is constant) or decreasing V (if Q is constant).
    • V = V₀/κ
    • C = κC₀
• Discharge of a capacitor through a resistor
  • Charge
    
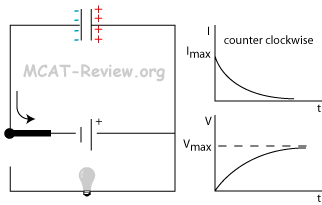
  • Discharge
    
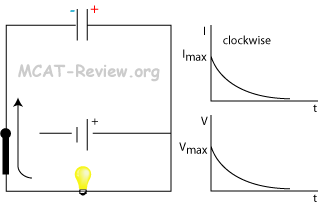
  • During the discharge of a capacitor, the capacitor acts as a battery and drives current flow, which decreases with time as the capacitor discharges.
• Conductivity theory
  • Conductivity is affected by electrolyte concentration:
    • No electrolyte, no ionization, no conductivity.
    • Optimal concentration of electrolyte, greatest conductivity due to greatest mobility of ions.
    • Too much electrolyte, ions are too crowded, less ion mobility, less conductivity.
  • Conductivity is affected by temperature:
    • In metals, conductivity decreases as temperature increases.
    • In semiconductors, conductivity increases as temperature increases.
    • At extremely low temperatures (below a certain critical temperature typically a few degrees above absolute zero), some materials have superconductivity - virtually no resistance to current flow, a current will loop almost forever under such conditions.
  • Conductivity (σ) is the inverse of resistivity (ρ).
  • Place a capacitor inside a solution, the solution will conduct a current between the plates of the capacitor, thus you can measure the conductivity of a solution using a capacitor.

Circuits

• Power in circuits (P = VI, P = I²R)
  • P = IV = I²R
  • P is power, I is current, V is voltage, R is resistance.
  • Power companies try to save the amount of copper needed for power lines by using thinner wires, which makes R quite high.
  • To minimize P dissipated by the wires, they minimize I by maximizing V. This is why power lines transfer electricity at high voltage.

Alternating Currents and Reactive Circuits

• Root-mean-square current
  • I_rms = ^I_max/_√2 = 0.7 I_max
• Root-mean-square voltage
  • V_rms = ^V_max/_√2 = 0.7 V_max
• V_rms = I_rmsR
• P_avg = I_rmsV_rms = I²_rmsR