|
|
Acid / base equilibria
- Bronsted definition of acid, base
- H-Acid + Base- ↔ Acid- + H-Base.
- From left to right:
- Acid: proton donor.
- Base: proton acceptor.
- Conjugate base: acid after losing its proton.
- Conjugate acid: base after gaining its proton.
- Ionization of water
- Kw, its approximate value (Kw = [H+][OH-] = 1*10^-14 at 25°C)
- H2O ↔ H+ + OH-
- At standard conditions, pure water dissociates to achieve [H+] = 10-7 M and [OH-] = 10-7 M.
- Kw = [H+] x [OH-] = 10-7 x 10-7 = 10-14
- definition of pH; pH of pure water
- pH = -log[H+]
- For pure water, pH = -log[10-7] = 7.
- Acidic: pH lower than 7.
- Neutral: pH = 7.
- Basic: pH higher than 7.
- pOH = -log[OH-].
- pH + pOH = 14.
- Conjugate acids and bases (e.g., amino acids)
| Acid |
Base |
↔ |
Conjugate base |
Conjugate acid |
| H2O |
H2O |
↔ |
OH- |
H3O+ |
| R-COOH |
H2O |
↔ |
R-COO- |
H3O+ |
| H2O |
R-NH2 |
↔ |
OH- |
R-NH3+ |
- More acidic ← +H3N-CH2-COOH ↔ +H3N-CH2-COO- ↔ H2N-CH2-COO- → more basic
- Strong acids and bases (common examples, e.g., nitric, sulfuric)
| Strong acid |
Formula |
| Perchloric acid |
HClO4 |
| Hydroiodic acid |
HI |
| Hydrobromic acid |
HBr |
| Sulfuric acid |
H2SO4 |
| Hydrochloric acid |
HCl |
| Nitric acid |
HNO3 |
| Hydronium ion |
H3O+ or H+ |
- Strong acids completely dissociate in solution.
- Complete dissociation occurs because the conjugate base anion is highly stable.
| Strong bases |
Formula |
| Lithium hydroxide |
LiOH |
| Sodium hydroxide |
NaOH |
| Potassium hydroxide |
KOH |
| Rubidium hydroxide |
RbOH |
| Cesium hydroxide |
CsOH |
| Calcium Hydroxide |
Ca(OH)2 |
| Strontium hydroxide |
Sr(OH)2 |
| Barium hydroxide |
Ba(OH)2 |
- Strong bases completely dissociate in solution.
- Complete dissociation occurs because the conjugate acid cation is highly stable.
- Weak acids and bases (common examples, e.g. acetic, benzoic)
| Weak acid |
Formula |
| Formic acid |
HCOOH |
| Acetic acid |
CH3COOH |
| Hydrofluoric acid |
HF |
| Hydrocyanic acid |
HCN |
| Hydrogen sulfide |
H2S |
| Water |
H2O |
- Weak acids partially dissociate in solution.
- Partial dissociation occurs because the conjugate base is fairly stable.
| Weak base |
Formula |
| Ammonia |
NH3 |
| Amine |
NR3 |
| Pyridine |
C5H5N |
| Ammonium hydroxide |
NH4OH |
| Water |
H2O |
- Weak bases partially dissociate in solution.
- Partial dissociation occurs because the conjugate acid is fairly stable.
- dissociation of weak acids and bases with or without added salt
- CH3COOH will dissociate less in a solution containing CH3COONa salt.
- NH4OH will dissociate less in a solution containing NH4Cl salt.
- This is due to Le Chatelier's principle: the hydrolysis of salts of weak acids will produce their conjugate bases, which reduces dissociation. Likewise, hydrolysis of salts of weak bases will produce conjugate acids.
- hydrolysis of salts of weak acids or bases
- Salt of weak acid:
CH3COONa ↔ CH3COO- + Na+
CH3COO- + H2O ↔ CH3COOH + OH-
- Salt of weak base:
NH4Cl ↔ NH4+ + Cl-
NH4+ + H2O ↔ NH3 + H3O+
- calculation of pH of solutions of salts of weak acids or bases
- Salt of weak acid:
- Let's say a solution contains M molar of CH3COONa.
- CH3COO- + H2O ↔ CH3COOH + OH-
- As M molar of CH3COO- start to abstract protons from the solvent:
- [CH3COO-] = M - x
- [CH3COOH] = x
- [OH-] = x
- Kb = Kw/Ka = [CH3COOH][OH-] / [CH3COO-] = x2/(M - x)
- Because x is very small, Kw/Ka = x2/M → solve for x.
- pOH = -log[OH-] = -log(x)
- pH = 14 - pOH.
- Salt of weak base:
- Let's say a solution contains M molar of NH4Cl.
- NH4+ ↔ NH3 + H+.
- As M molar of NH4+ dissociates:
- [NH4+] = M - x
- [NH3] = x
- [H+] = x
- Ka = Kw/Kb = [NH3][H+] / [NH4+] = x2/(M - x)
- Because x is very small, Kw/Kb = x2/M → solve for x.
- pH = -log[H+] = -log(x).
- Equilibrium constants Ka and Kb: pKa, pKb
- H-Acid ↔ H+ + Acid-
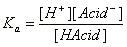
- Base + H2O ↔ H-Base+ + OH-
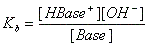
note: water is not included in the formula because it is not a solute.
- Ka x Kb = Kw = 10-14
- pKa = -log Ka
- pKb = -log Kb
- pKa + pKb = 14
- Buffers
- definition and concepts (common buffer systems)
- Buffers = Solutions that resist changes in pH.
- Salts of weak acids and bases form buffer systems.
- A buffer system consists of an equilibrium between an acidic species and a basic species. Note the "equilibrium", you can't just dump HCl and NaOH together and expect buffering, because neutralization will occur and the acidic species and the basic species won't be at an equilibrium.
- The concept is that acidic species of the buffer system will donate protons to resist increases in pH, while the basic species of the buffer system will accept protons to resist decreases in pH.
- Buffer systems formed by weak acids have maximum buffering capacity at the pH = pKa of the acid.
- When [acid] = [conjugate base], the system is buffered at pH = pKa of the acid.
- Buffer systems formed by weak bases have maximum buffering capacity at the pH = 14 - pKb of the base.
- When [base] = [conjugate acid], the system is buffered at pH = 14 - pKb of the base.
- influence on titration curves
- Buffers make the titration curve "flat" at the region where buffering occurs. On a titration curve, this is the point of inflection.
- The point of inflection is at pH = pKa (or 14 - pKb) of the buffer.
- The area around the point of inflection is the region where the solution has buffering capacity. The pH of this buffering region is typically pKa +/- 1 (or 14 - pKb +/- 1).
Titration
- Indicators
- H-In ↔ H+ + In-
- Ka = [H+][In-] / [H-In]
- Indicators behave just like weak acids/bases.
- The indicator is present in such a small amount that it doesn't affect the solution's pH.
- When the solution has a low pH (high [H+]), the indicator is mostly in the H-In form, which is of one color.
- When the solution has a high pH (low [H+]), the indicator is mostly in the In- form, which is of another color.
- Neutralization: Acid + Base = Salt + Water.
- Interpretation of titration curves
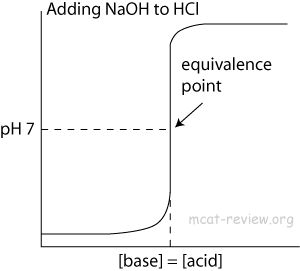
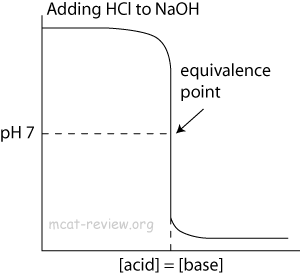
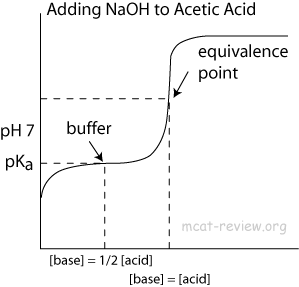
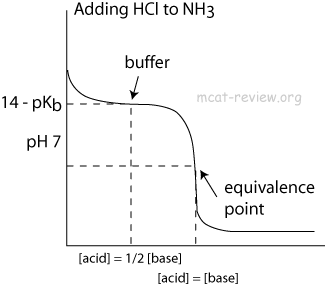
- At the point of inflection (buffer arrow), the [acid] = [conjugate base] or [base] = [conjugate acid], pH = pKa, and [titrant] = 1/2 [weak acid/base]
- The buffer region has pH values of pKa +/- 1.
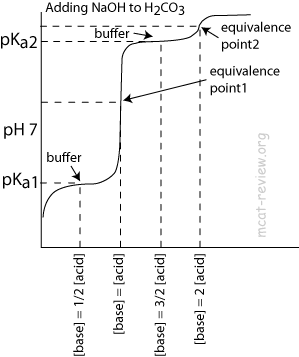
- Polyprotic acids have multiple pKa, points of inflection, and equivalence points.
- Like monoprotic acids, each point of inflection corresponds to the pKa for the acidic species.
- At each pKa, [acidic species] = [conjugate base of the acidic species].
- For H2CO3:
- pKa1: [H2CO3] = [HCO3-]
- Equivalence point 1: almost everything is HCO3-
- pKa2: [HCO3-] = [CO32-]
- Equivalence point 2: almost everything is CO32-
- Redox titration
- While Bronsted acid-base titrations involve proton transfers, redox titrations involve electron transfers.
- Redox = reduction + oxidation = species A gains electrons + species B lose electrons.
- Reduction = reduction in charge = decreased oxidation number = gaining electrons.
- Oxidation = increase in charge = increased oxidation number = losing electrons.
- 5H2O2 + 2MnO4- + 6H+ → 2Mn2+ + 5O2 + 8H2O
- Normally oxygen has an oxidation state of -2, but in peroxides, it is -1. The reactants here include a peroxide.
- Oxygen, and anything else in its elemental state has an oxidation number of 0. The product O2 is one such case.
- Hydrogen is always +1 unless it is a hydride, in which case it's negative 1. For this reaction, all hydrogens are +1.
- Doing some math, we find that the reactant Mn has an oxidation number of +7.
- The half reactions (reactions that depict electron transfer only) are as follows:
- Reduction: Mn7+ + 5e- → Mn2+
- Oxidation: O- → O0 + e-
|
|
